本文へスキップ

新潟県工業技術総合研究所は、工業系の技術支援機関です。



Topページ　>　機械・金属関係　技術トピックス 　>　Ｘ線応力測定における応力値のばらつきについて
Ｘ線応力測定における応力値のばらつきについて

１．はじめに
　材料を機械加工や熱処理することによって生じる残留応力は、加工後の製品の寸法精度、静的および疲労強度、耐食性などに大きい影響を及ぼします。このため、熱処理による残留応力の除去や、疲労強度を高めるためのショットピーニングや高周波焼入れなどを行い、積極的に製品表面に圧縮の残留応力を生じさせること等が行われています。残留応力を精度よく測定することは、外力によって生じる応力測定に比べて難しい場合が多く、いまだに多くの問題が残されています。
　Ｘ線の回折現象を利用したＸ線応力測定法は、Ｘ線回折にあずかる体積中の平均的な応力を測定できます。この測定法は、外力によって生じた応力も測定できますが、主な用途は残留応力測定です。
　この測定法では、試料にＸ線を照射した際、回折してくるＸ線の強度を計測して回折線の位置や応力値等を測定しますが、これらの測定値はＸ線強度固有の統計変動によってばらつきを生じることが分かっています。この統計変動はＸ線による測定値には避けられないものです。このため、測定値の信頼性を高めるには、Ｘ線強度固有の統計変動によって生じる測定値のばらつきの大きさを表す標準偏差を求めて、測定値の再現性を検討することが重要となります。
　測定される応力値などの測定値の標準偏差は、一回の測定から統計学の理論を用いて求める方法が提案されています1)～4)。この方法を適用するには、Ｘ線応力測定装置で計測したＸ線計数値のばらつきの大きさが、理論式に従っていることを確認する必要があります。
　ここでは、工業技術総合研究所が昨年度導入したＸ線応力測定装置を用いて、先ずＸ線計数値のばらつきの大きさが理論式に従っていることを確認しました。次に文献1)～4)の理論により求めた応力値の標準偏差と、繰り返し測定した応力値の標準偏差を比較し、両者がほぼ一致することを確認しました。

２．Ｘ線強度の統計変動
　応力値のばらつきの大きさを表す標準偏差は、ばらつきの主な原因であるＸ線強度の統計変動から解析的に求めることができます。このＸ線計数値yの母分散σy2と母平均μyとの間には、理論上
　　　σy2＝μy・・・(1)
が成り立ちます5)。
　本実験では、昨年度導入したＸ線応力測定装置を用いて、表1に示すプリセットタイムで回折するＸ線の強度yを各条件で100回測定し、yの平均値、分散、標準偏差および相対誤差を求めました。yの平均値Yに対する標本分散Sy2、標本標準偏差Sy、相対誤差Sy/Yの変化をそれぞれ図1～図3に示しました。
　Ｘ線応力測定に用いるＸ線強度は、概ね3×103～105の範囲です。図3より、この範囲のＸ線の強度yの相対誤差Sy/Yは0.01以下（1％以下）と小さいことが分かりますので、Y≒yとなります。このことから、図1～図3より
　　　Sy2＝y・・・(2)
　　　Sy＝y0.5・・・(3)
　　　Sy/y=y-0.5・・・(4)
となります。
　また100個の測定値yから求めた標本分散Sy2は、標本数が100と多いため、yの母分散σy2にほぼ等しいと考えられます。したがって、式(2)～(4)より次式が得られます。
　　　σy2＝y・・・(5)
　　　σy＝y0.5・・・(6)
　　　σy/y=y-0.5・・・(7)
式(5)～(7)より、Ｘ線強度の標準偏差σyはそのＸ線強度の平方根y0.5で表すことができます。また、強度が高くなるにつれて、その相対誤差σy/yは小さくなる（y-0.5倍となる）ことが分かります。
　式(5)は理論式(1)と同じであるため、実験で用いた装置はＸ線強度の統計変動を正しく表すことができます。

表1　Ｘ線強度の統計変動の測定条件
測定装置（株）リガク製 Ｘ線応力測定装置 PSPC-MSF-3M
管球Cr
Kβフィルタ V
管電圧30 kV
管電流10 mA
コリメータ2×2 mm
ψ角0 deg
2θ角142-170 deg
ステップ角0.05 deg
プリセットタイム1, 5, 10, 50, 100 sec
測定試料鉄粉末
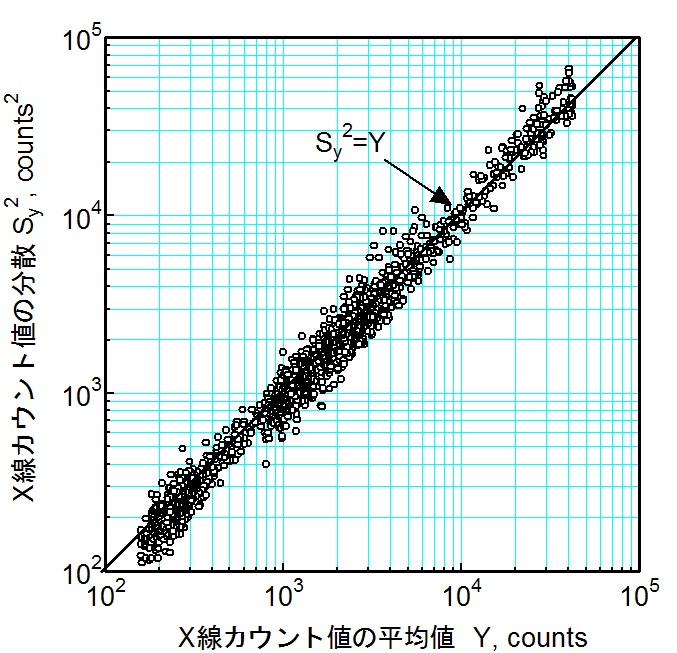
Ｘ線強度の分散とその平均値
図1　Ｘ線強度の分散とその平均値

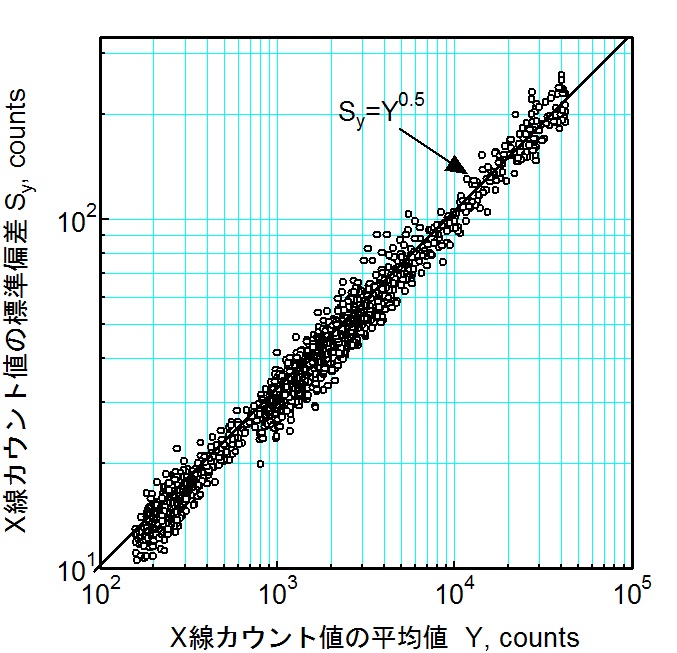
Ｘ線強度の標準偏差とその平均値
図2　Ｘ線強度の標準偏差とその平均値

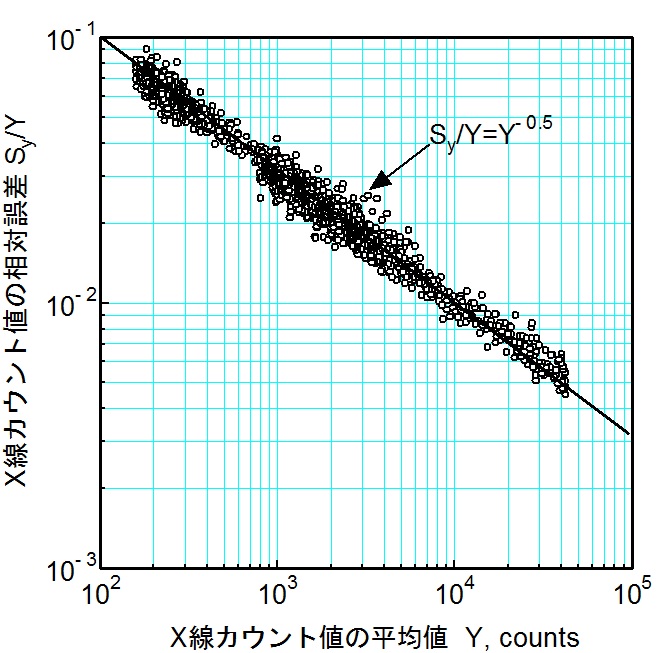
Ｘ線強度の相対誤差とその平均値
図3　Ｘ線強度の相対誤差とその平均値

３．Ｘ線応力値の統計変動
　文献1)～4)の理論および従来法から求めた応力値の標準偏差と、同じ測定を100回測定した測定値から求めた応力値の標準偏差を比較しました。測定条件を表2に示します。ここで、文献1)～4)の理論と従来法において、応力値の標準偏差を求める上での大きな違いは、従来法はsin2ψ線図の直線回帰におけるt分布の式から求めていますが、文献1)～4)の理論はばらつきの主な原因であるＸ線強度の統計変動から解析的に求めている点です。
　図4に、100回測定した結果を示します。図に示したエラーバーは、文献1)～4)の理論によって求めた応力値の95%信頼区間です。エラーバーの中に100回測定した平均値がほぼ含まれていることが分かります。さらに、図より100回の測定値の95％信頼区間とエラーバーの幅がほぼ一致していることから、1回の測定で得られる信頼区間は100回測定したときのばらつきの大きさをよく表していることが分かります。
　一方、図5には、従来法によって求めた応力値の95％信頼区間をエラーバーに示しました。測定値のばらつきの大きさに比べて、各測定値のエラーバーの大きさはかなり大きく、測定値のばらつきを正しく表していないことが分かります。


表2　Ｘ線応力値の統計変動の測定条件
測定装置（株）リガク製 Ｘ線応力測定装置 PSPC-MSF-3M
管球Cr
Kβフィルタ V
管電圧30 kV
管電流10 mA
コリメータ2×2 mm
sin2ψ0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6
2θ角142-170 deg
ステップ角0.2 deg
プリセットタイム30 sec
ピーク位置決定法ガウス曲線法
バックグラウンド補正あり
LPA因子補正あり
応力定数-318 MPa/deg
信頼区間95 %
測定試料S45C焼入材
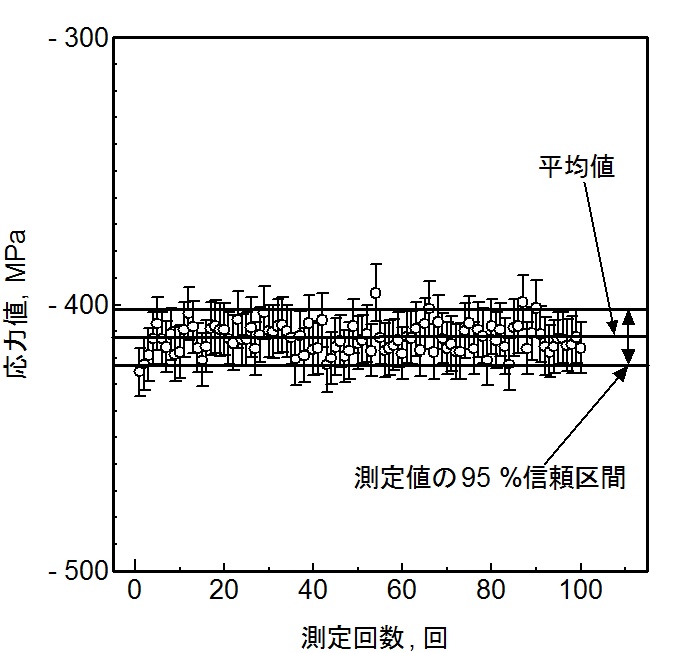
同一条件による応力測定結果（X線強度の統計変動）
図4　同一条件による応力測定結果（Ｘ線強度固有の統計変動から信頼区間を求めたもの）

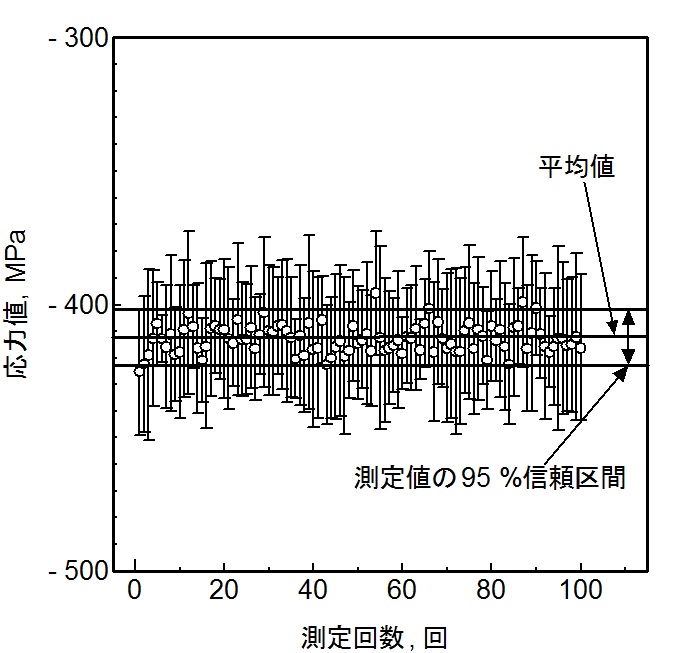
同一条件による応力測定結果（従来法）
図5　同一条件による応力測定結果（従来法から信頼区間を求めたもの）

文献
1)Kurita, M., Journal of Testing and Evaluation, 9-5 pp.285-291, (1983).
2)Kurita, M., Bulletin of the JSME, 21-156, pp.955-962, (1978).
3)Kurita, M., Journal of Testing and Evaluation, 10-2 pp.38-46, (1982).
4)栗田ほか, 材料, 31-345, pp.609-615, (1982).
5)三浦ほか, 放射線計測学（1970）, pp.325-328, 裳華房.

 問い合わせ：新潟県工業技術総合研究所
　　　　　　 県央技術支援センター 　　斎藤　雄治
　 　　　　　TEL：0256-32-5271　　FAX：0256-35-7228