新潟県工業技術総合研究所は、工業系の技術支援機関です。

Topページ　>　機械・金属関係　技術トピックス 　>　Ｘ線回折における積分強度のばらつきについて

Ｘ線回折における積分強度のばらつきについて

１．はじめに

　X線応力測定装置は結晶材料表面の局所の応力を測定しますが、同時に積分強度なども求めることができます。積分強度などについてもX線で測定される値のため、応力と同様に、X線強度固有の統計変動によりばらつきを生じると考えられます。
　ここでは、X線強度固有の統計変動による積分強度のばらつきの大きさを一回の測定から計算で求める方法を示すとともに、実際に測定した結果を紹介します。なお、積分強度のばらつきの計算方法については、文献¹⁾と同様な方法により行っています。

２．積分強度のばらつきの計算

　図1に示すように、回折角$x$に対する回折X線強度$y_0$、$y_1$、・・・、$y_n$、$y_{n+1}$をステップ角cの間隔で測定した場合を考えます。いま、バックグラウンド強度$y_b$を回折線の両端の点（$x_0$, $y_0$）と（$x_{n+1}$, $y_{n+1}$）を結んだ直線で表すものとすれば
\[ y_{bi}=E_iy_0+F_iy_{n+1} \tag{1} \] ここに
\[ E_i=\frac{x_{n+1}-x_i}{x_{n+1}-x_0} \tag{2} \] \[ F_i=\frac{x_i-x_0}{x_{n+1}-x_0} \tag{3} \] となります。ここに、添字$i$は0～$n+1$の値を取ります。
　いま、図2に示すように、X線強度$y$をバックグランドとLPA因子で補正した値を$z$で表すと、$z$は次式となります。 \[ z_i=l_i(y_i-E_iy_0-F_iy_{n+1}) \tag{4} \] ここに、$l_i$はLPA因子の逆数です。
　回折X線強度分布の積分強度$I$は、$i=0$～$n+1$の点（$x_i$, $z_i$）より計算した積分値として次式のように表されます。 \[ I=\int z(x)dx \tag{5} \] 式(5)の積分値は近似的に次式から計算されます。 \[ I=c\sum_{i=1}^{n} z_i \tag{6} \] $y$の統計変動によって生じる積分強度$I$のばらつきの大きさを表す分散$\sigma^2_I$は、統計学の理論によって次式から求めることができます。 \[ \sigma^2_I=\sum_{i=0}^{n+1} \left(\frac{\partial I}{\partial y_i}\right )^2 \sigma^2_{yi} \tag{7} \] ここで、次式が成り立ちます。 \[ \sigma^2_y=y \tag{8} \] 式(8)を式(7)に代入すると次式となります。 \[ \sigma^2_I=\sum_{i=0}^{n+1} \left(\frac{\partial I}{\partial y_i}\right )^2 y_i \tag{9} \] 式(9)に式(4)と(6)を代入して$\partial I/\partial y_i$を求めます。今後は簡単のため、$i=1$～$n$までの和を取ることを単に$\sum$と表すこととします。はじめに、$i=0$については
\[ \frac{\partial I}{\partial y_0}=-c\sum l_i E_i \tag{10} \] となります。次に、$i=1～n$については \[ \frac{\partial I}{\partial y_i}=c l_i \tag{11} \] となり、さらに、$i=n+1$については \[ \frac{\partial I}{\partial y_{n+1}}=-c\sum l_i F_i \tag{12} \] となります。式(10)～(12)を式(9)に代入すると \[ \sigma^2_I=c^2 \left[ (\sum l_i E_i)^2 y_0 + \sum l_i^2 y_i + (\sum l_i F_i)^2 y_{n+1} \right ] \tag{13} \] を得ます。
　式(6)と(13)において、X線強度すなわちプリセットタイムを$k$倍にすると、$c$、$E_i$、$F_i$は変わりませんが、$y_i$や$z_i$は$k$倍になります。このため、プリセットタイムを$k$倍にすると、$I$は$k$倍になり、$I$の標準偏差$\sigma_I$は$\sqrt{k}$倍になることが分かります。なお、LPA因子補正を行わない場合は式(13)の$l_i$を1と置きます。



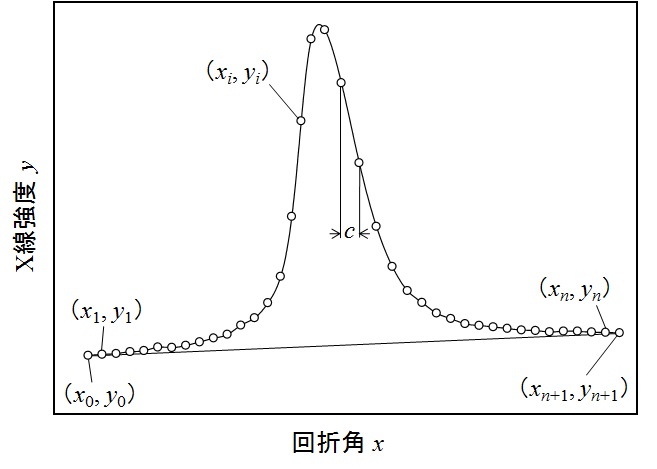
図1　X線強度$y$と回折角$x$の関係


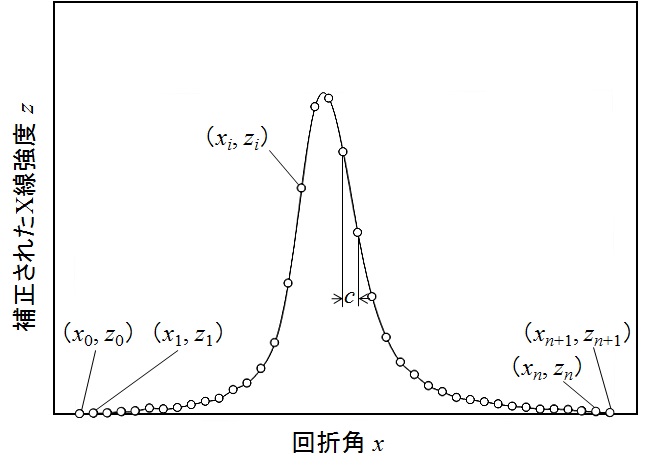
図2　補正されたX線強度$z$と回折角$x$の関係

３．実験方法

　ここでは、「Ｘ線応力測定における応力値のばらつきについて」の2節において、プリセットタイム1、5、10、50および100sに対して、それぞれ同条件で100回測定した純鉄の回折X線強度分布を使って積分強度を計算しました。積分強度の計算には、回折X線強度分布のデータのうち回折角が150～164degの範囲を用いました。X線強度はバックグラウンドとLPA因子で補正しました。1回ごとの回折X線強度分布から式(13)で求めた積分強度の標準偏差と、100個の積分強度の標準偏差を比較しました。

４．実験結果および考察

　図3に、測定した回折X線強度分布の一例を示します。図より、回折角が156deg付近にピーク強度をもつ回折線が得られていることが分かります。プリセットタイム1、10、50および100sについても同様な回折X線強度分布が得られました。
　図4～図8に、プリセットタイムを1、5、10、50および100sで100回ずつ積分強度を測定した結果を示します。図には、100個の積分強度の平均値と95％信頼区間を示しました。また、一回ごとの測定から式(13)を使って計算した積分強度とその95％信頼区間をエラーバーで示しました。これらの図より、エラーバーの中に100回測定した平均値がほぼ含まれていることが分かります。
　表1に、各プリセットタイムに対して
①100個の積分強度の平均値とその95％信頼区間
②一回ごとに計算で求めた積分強度の95％信頼区間の100個の平均値
を示しました。表1において、①と②いずれもプリセットタイムの平方根にほぼ比例して変化することが分かります。また、同一のプリセットタイムにおいて、②は①に近い値を取っていることが分かります。これらの結果により、式(13)は積分強度のばらつきの評価に有効と考えられます。
　ここでは、式(13)を使って積分強度の標準偏差を計算で求める方法を紹介しました。この方法を使うことで、積分強度を利用した残留オーステナイトの測定値のばらつきの評価等に応用できると考えられます。


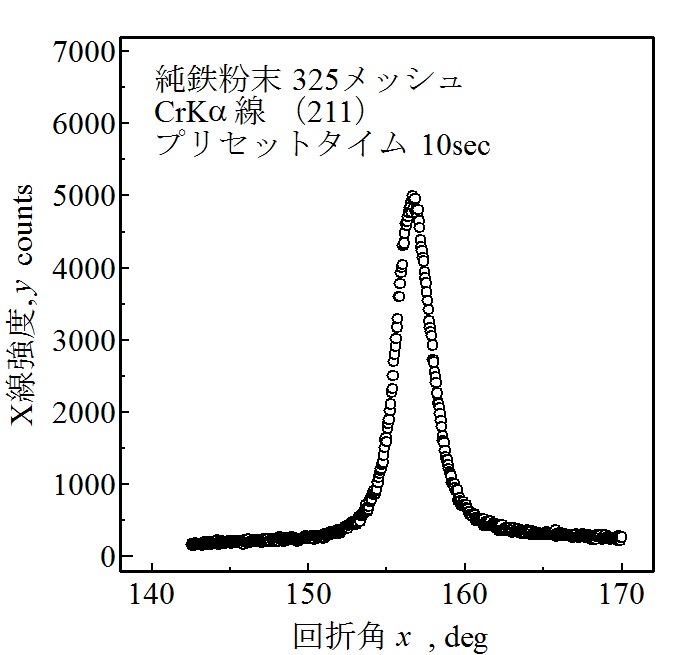
図3　測定した回折X線強度分布の一例（プリセットタイム10s）


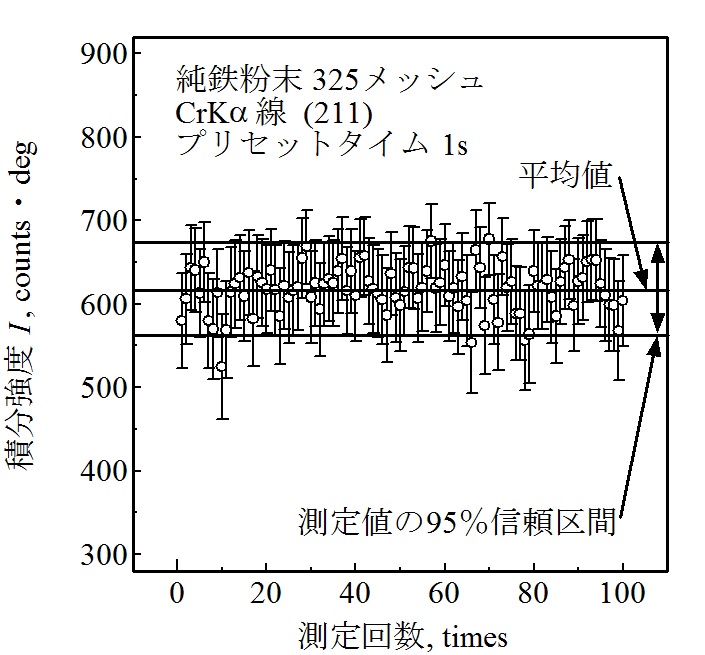
図4　プリセットタイム1sの積分強度の統計変動


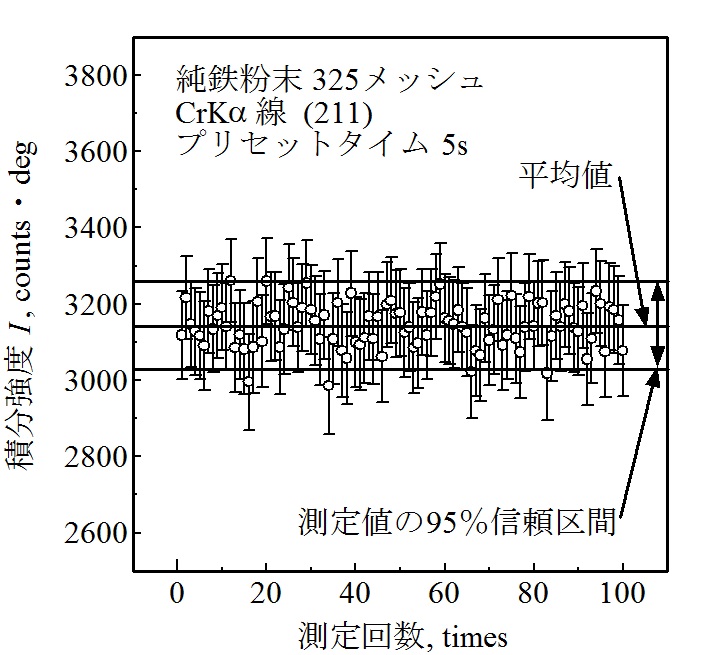
図5　プリセットタイム5sの積分強度の統計変動


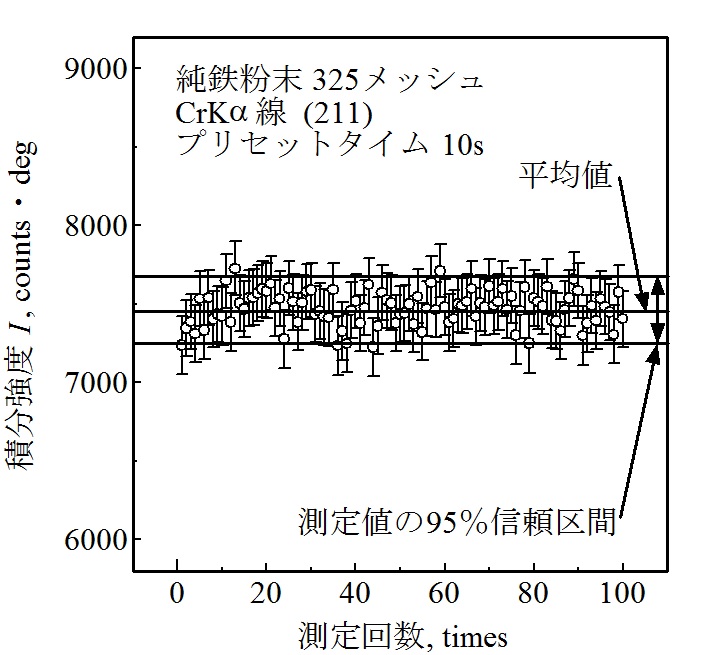
図6　プリセットタイム10sの積分強度の統計変動


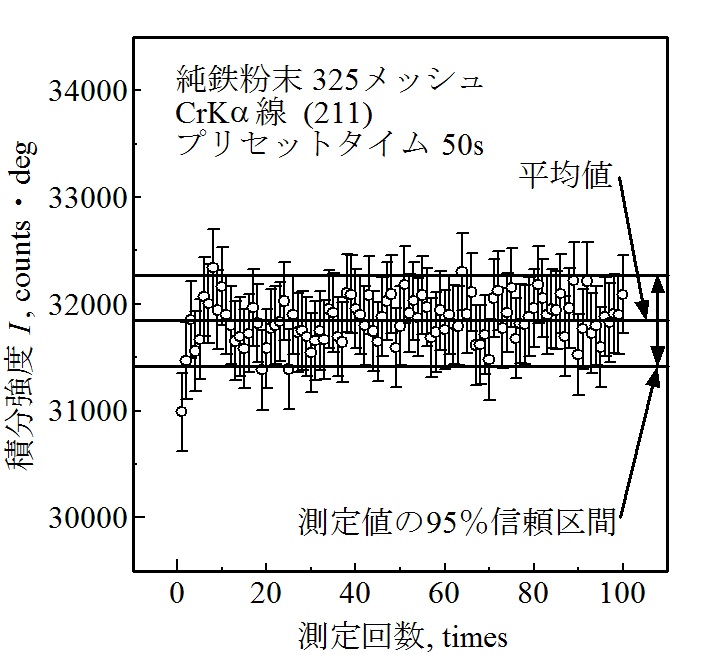
図7　プリセットタイム50sの積分強度の統計変動


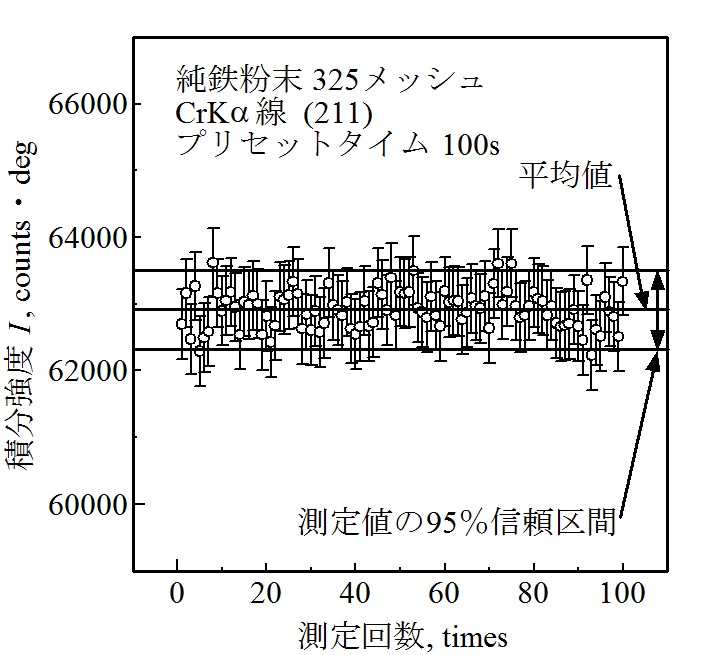
図8　プリセットタイム100sの積分強度の統計変動



表1　X線による積分強度とその95％信頼区間

	①100個の積分強度		②1回ごとに解析的に求めた積分強度の95％信頼区間
プリセットタイム, s	平均値, counts・deg	95％信頼区間, counts･deg	100個の平均値, counts･deg
1	618	±56	±53
5	3144	±116	±116
10	7470	±218	±178
50	31843	±433	±369
100	62922	±570	±518

文献

1)栗田ほか, 材料, 31-345 pp.609-615, (1982).

問い合わせ：新潟県工業技術総合研究所 　　　　　　 県央技術支援センター 　　斎藤　雄治 　 　　　　　TEL：0256-32-5271　　FAX：0256-35-7228